|
این مطلب از بخش آموزش وب‌سایت المپیاد کامپیوتر رشد،انتخاب شده که با فرمت pdf نیز در وب‌سایت المپیاد رشدموجود می‌باشد. برای مشاهده این موضوعات در وب‌سایت المپیاد، به آدرس فهرست مطالب کامپیوتر مراجعه کنید. همچنین می‌توانید با کلیک اینجا ، با ویژگی‌های بخش آموزش این وب‌سایت آشنا شوید. |
گراف های مسطح
در مقدمه دیدیم که گراف
را می توانید روی سطح کاغذ به گونه ای کشید که هیچ دویالی یکدیگر را قطع نکنند. به این گونه گرافها، گراف مسطح گوییم:
تعریف
گراف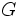
را یک گراف مسطح گوییم هر گاه بتوان آن را روی سطح صاف ( و یا روی سطح کره ) به گونه ای رسم کرد که هیچ دو یالی یکدیگر را قطع نکنند.
همان گونه که در تعریف می بینید، در واقع مسطح بودن گراف معادل است با این که گراف را بتوان روی کره رسم کرد. این که گراف را روی کره ترسیم کنیم، فوایدی حاصل می آورد که در برخی محاسبات آنها خواهیم دید.
و اما اولین سوالی که به ذهن خطور می کند این است که آیا هر گرافی، یک گراف مسطح است یا نه؟! اگر همان طور که در مقدمه آمد سعی کرده باشید گراف
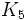را روی صفحه رسم کنید ( از این به بعد منظور از رسم کردن گراف روی صفحه این است که گراف طوری رسم شود که هیچ دو یالی همدیگر را قطع نکنند ). حتی اگر مدت زیادی به آن ور رفته باشید شکست خورده اید. کمی بعد ( همین بخش، به کمک برخی تکنیکها و قضایا اثبات خواهیم کرد که 
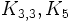و بسیاری گرافهای دیگر مسطح نیستند. البته برای اینکه کمی قانع شوید نامسطح بودن 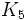را همان طوری که در زیر ذکر شده است،می توانید به طور شهودی قبول کنید:
یک گراف
روی صفحه رسم می کنیم و نواحی بین یالها را برای روشنتر شدن رنگ می کنیم:
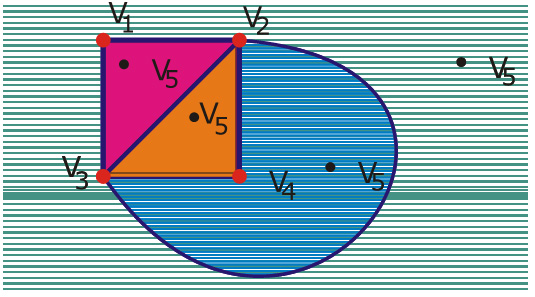
می دانیم که
جزیی از گراف 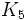است پس برای رسم یک گراف 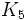کافیست که یک راس 
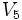به بیفزاییم سپس با کامل کردن گراف و رسم یالهای باقی مانده، گراف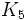 را بدست آوریم. همان گونه که در شکل می بینید راس 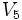در یکی از نواحی سبز، آبی، نارنجی یا بنفش باید بیافتد چرا که جز این 4 ناحیه، ناحیه ی دیگری در صفحه نداریم!
حال با آزمون و خطا مساله برایمان روشن خواهد گشت. مثلاً فرض کنید در ناحیه ی به رنگ نارنجی باشد. آیا می توانید
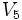را به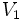 
رسم کنید طوری که با هیچ یالی برخورد نداشته باشد؟ من که این طور فکر نمی کنم! بررسی بقیه نواحی را برعهده ی شما می گذارم. حال باید به من حق بدهید که که بگویم:
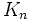گراف مسطح نیست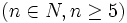
مساله
مانند روشی که برای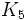 ذکر شد و به طور شهودی اثبات کنید که 
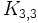و نیز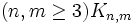
گراف مسطح نیستند.
•لازم به ذکر است که از قضیه مربوط به توپولوژی که بالا استفاده کردیم با عنوان قضیه ی خم ژردان
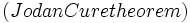که بیان می دارد از یک خم بسته روی صفحه یک نقطه را از درون خم نمی توان به نقطه ای خارج از خم با خطی وصل کرد طوری که خط واصل دو نقطه خم را قطع نکند.