| حرکت مستقیم الخط یکنواخت به حرکتی گفته می‌شود که در آن سرعت ثابت باشد، در سرعت متوسط در این حرکت در هر فاصله زمانی دلخواه یکسان و برابر سرعت متحرک است. ممکن است جابجاییهای متحرک روی خط راست در زمانهای مساوی باهم مساوی باشند، اما سرعت متحرک ثابت نباشد، در نتیجه حرکت یکنواخت نباشد. اما اگر حرکت یکنواخت باشد، جابجایی متحرک در زمانهای مساوی باهم مساوی است. |
|
دید کلی
حرکت تند و کند برای هر کس واژه‌ای آشناست، اما برای بیان تمایز آنها دو راه متفاوت وجود دارد. در ورزشهای میدانی می‌گوییم دونده a از دونده b تندتر می‌رود، هر گاه a همان مسافت b را در زمان کمتری بدود. اما وقتی که گفته می‌شود در بزرگراه می‌توانید تندتر رانندگی کنید، به این معنی است که شما مجاز هستید نسبت به حرکت در یک جاده فرعی کیلومترهای بیشتری را در یک ساعت طی کنید. با استفاده از نموداری که مکان را به عنوان تابعی از زمان نشان می‌دهد. می‌فهمیم که جه وقت جسم تند یا کند حرکت کرده است، این کار را با روش مقایسه جابجاییها در فاصله‌های زمانی مساوی انجام می‌دهیم.
معادله حرکت یکنواخت
معادله مکان این متحرک نسبت به زمان تابع درجه اولی است. در این رابطه
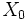
مکان اولیه متحرک از مبدا محور مکان در لحظه شروع حرکت
،
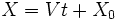
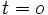
است. اگر
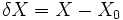
و
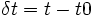
داریم:
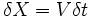
که دراین رابطه
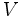
تندی است، چون
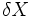
دیمانسیون (بعد) طول و
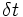
دیمانسیون زمان دارد،
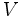
دیمانسیون طول تقسیم بر زمان یا طول در واحد زمان خواهد داشت. واحد تندی بستگی به واحدهایی دارد که برای جابجایی و زمان بکار گرفته شده‌اند.
مثلا اگر
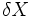
بر حسب
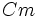
و
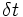
بر حسب ثانیه بیان شده باشد،
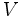
بر حسب
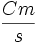
معین می‌شود. اگر
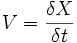
معیاری برای سراشیبی بخش مستقیم نمودار
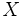
نسبت به
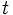
است و آن را شیب خط می‌نامند. هر گاه نسبت دو تغییر مورد نظر باشد، منظور این است که تغییر صورت کسر در طول فاصله زمانی مخرج کسر صورت می گیرد.
از اینرو
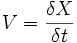
به این معنی است که برای یافتن سرعت ، تغییر مکان
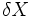
را به فاصله زمانی
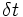
که در جریان آن تغییر مکان مورد نظر صورت گرفته است. تقسیم می‌کنیم. حالت خاص حرکت یکنواخت اگر در مبدا زمان (
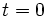
) متحرک در صدابر باشد (یعنی
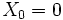
) معادله حرکت بصورت
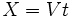
در می‌آید.
تعیین سرعت متوسط در حرکتهای یکنواخت متوالی
اگر متحرکی جابجایی
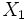
را با سرعت
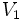
و جابه جایی
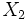
را با سرعت
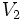
و ... طی کند،
سرعت متوسط در کل جابجایی برابر مجموع جابجاییها بر مجموع زمانهای طی این جابجاییها خواهد بود، که چون زمان مربوط به هر جابجایی در دست نیست، بوسیله
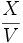
زمان مربوط به هر جابجایی بدست می‌آید.
- حالت خاص: اگر متحرکی
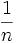مسیری را با سرعت 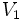و بقیه را با سرعت 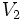طی کند، سرعت متوسط بوسیله رابطه 
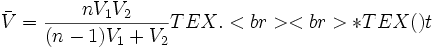: سرعت 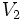، 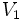و ... طی کند سرعت مرتبط برابر است با معدل سرعتها.
مسائل حرکت نسبی
هر گاه دو متحرک باهم در حرکت باشند، برای بررسی مسائل مربوطه دو طریق زیر می‌توان عمل کرد:
- معادله حرکت هر کدام را جداگانه و با توجه به صورت مساله با یکدیگر ترکیب کرد.
- یکی از آنها را ساکن فرض کرده و معادله حرکت نسبی را نوشته و مساله را حل و با توجه به اینکه در دو حرکت هم امتداد و مختلف الجهت سرعت نسبی برابر است با مجموع سرعتها و در دو حرکت هم امتداد و هم جهت سرعت نسبی برابر است با تفاضل سرعتها.
مباحث مرتبط با عنوان
