مقدمه
برای تحلیل واریانس تصمیم گیری دربارهی این امر را مورد توجه قرار میدهیم که آیا تفاوتهای مشاهده شده بین بیش از دو میانگین نمونهای را میتوان معلول تصادف دانست و یا اینکه بین میانگینهای جامعههای مورد نمونهگیری تفاوتهای واقعی وجود دارند. مثلا ممکن است بخواهیم بر مبنای دادههای نمونهای تصمیم بگیریم که آیا واقعا تفاوتی بین میزان مؤثر بودن سه روش تدوین یک زبان خارجی موجود است یا خیر. یا بخواهیم میزان متوسط محصول در هر جریب برای شش نوع مختلف گندم را مقایسه کنیم. چون اختلافهایی که مشاهده میشوند میتوانند همواره معلول عواملی بجز عوامل مشخصی باشند- مثلا اختلاف در وضع یادگیری دانشآموزانی که تحت آموزش سه روش مختلف هستند میتواند ناشی از اختلاف هوش آنها باشد- ما برخی سوالات مربوط به طرح آزمایشها را نیز مورد بحث قرار میدهیم تا با درجه اطمینان معقولی ، نتایج معنیدار آماری را بتوان به علل مشخصی نسبت داد.
تعریف واریانس
از
امید ریاضی میدانیم که
گشتاور 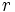
ام حول میانگین متغیرتصادفی
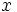
، که آن را با

نشان میدهیم، مقدار امید

است؛ بدین ترتیب

را
واریانس توزیع
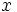
یا صرفا واریانس
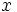
مینامند و آن را با

،

یا

نشان میدهند.
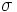
، ریشه دوم مثبت واریانس را
انحراف معیار مینامند. با توجه بشکل مشخص است که چگونه واریانس ، منعکسکننده پراکندگی توزیع متغیر تصادفی است. همانطور که دیده میشود، یک مقدار کوچک

این نکته را القا میکند که بدست آوردن مقداری نزدیک میانگین محتملتر است، و یک مقدار بزرگ

، این نکته را القا میکند که بدستآوردن مقداری که نزدیک میانگین نیست احتمال زیادی دارد. بطور کلی نتیجهای که میتوان گرفت این است که هر چه واریانس کم باشد پراکندگی اطراف میانگین کم است.
نکته
اضافهکردن مقداری ثابت به متغیر تصادفی که نتیجه آن انتقال تمام مقادیر به چپ یا به راست است، به هیچ وجه اثری بر پراکندگی توزیع آن ندارد. همینطور اگر متغیر تصادفی را در ثابتی ضرب کنیم. واریانس در مربع آن ثابت ضرب میشود که موجب تغییر متناظری در پراکندگی توزیع میشود. بطور کلی قضیه زیر را میآوریم:
قضیه
اگر واریانس
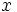
برابر

باشد، آنگاه

.
تحلیل واریانس یک طرفه
در حالت کلی در چنین مسائلی ،
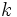
نمونه تصادفی مستقل به اندازه
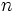
از
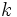
جامعه داریم و مقدار

ام با

نشان داده میشود و فرض خواهیم کرد که متغیرهای تصادفی متناظر یعنی

ها ، که همه مستقلاند دارای توزیعهای نرمال با میانگینهای مربوط

، و واریانس مشترک

باشند. با بیان این فرضها بگونهای نسبتا متفاوت ، میتوانیم بگوئیم که مدل مشاهدات با عبارت

به ازای

و

داده میشود که در آن

ها مقادیر

متغیر تصادفی نرمال با میانگینهای صفر و واریانس مشترک

هستند. برای آنکه امکان تعمیم این مدل به انواع وضعیتهای پیچیدهتر موجود باشد معمولا آن را با

می نویسند در اینجا

به میانگین کل اطلاق میشود و

ها که
اثرهای تیماری ، نامیده میشوند، چناناند که

.
چون به ازای هر
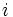
،

ها مقادیر نمونهای تصادفی به اندازه
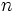
از جامعه نرمالی با واریانس

است، نتیجه میشود که به ازای هر i

.
یک متغیر تصادفی خیدو با
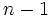
درجه آزادی است. به علاوه چون این
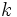
متغیر تصادفی مستقلاند نتیجه میشود که

یک
متغیرتصادفی خیدو با

درجه آزادی است. چون میانگین توزیع خیدو دو برابر درجه آزادی آن است، نتیجه میگیریم که عبارت بالا مقدار یک متغیر تصادفی با میانگین

است. بنابراین سیگماهای فوق تقسیم بر

را میتوان بعنوان برآورد

بکار برد. این کمیت را
میانگین مربعات خطا نامیده و با MSE نشان میدهند.
تحلیل واریانس دو طرفه
اساسا دوره مختلف در تحلیل آزمایشهای دو متغیره وجود دارد و راهها بستگی به این دارند که آیا متغیرها مستقلاند یا تأثیر متقابل دارند. برای آنکه منظور خود را از "تأثیر متقابل" روشن کنیم فرض میکنیم که یک سازنده لاستیک اتومبیل آجهای مختلف را آزمایش میکند و به این نتیجه میرسد که یک نوع آنها مناسب جاده خاکی و نوع دیگر مناسب جاده آسفالته است. اگر چنین باشد، گوئیم که بین شرایط جاده و طرح آن آج تاثیر متقابل وجود دارد. در اینگونه مسائل برای بررسی اینکه آیا اختلاف بین میانگینها برای مسیرهای مختلف معنیدار هستند یا نه با تحلیل واریانس دو طرفه سر و کار خواهیم داشت.
کاربردها
تحلیل واریانسها در صنعت ، مهندسی کشاورزی ، اقتصاد - علوم انسانی و اجتماعی از اهمیت خاصی برخوردار است. برای مثال در مورد کشاورزی به ذکر یک مثال میپردازیم: فرض کنید میخواهیم 25 نوع گندم و در همان حال تاثیر 12 کود مختلف را با هم مقایسه کنیم. برای انجام آزمایشی که در آن هر یک از 25 نوع گندم در ارتباط با هر یک از 12 کود بکار میروند باید 300 قطعه زمین را بکاریم و میتوان به آسانی تصور کرد که یافتن این همه قطعه زمین که برای آنها ترکیب خاک ، آبیاری ، شیب و ... ثابت یا قابل کنترل باشد تا چه اندازه مشکل است. در نتیجه به طرحهایی نیازمندیم که درباره پارامترهای مربوط به مدل آزمون کردن فرضهایی را بر مبنای آزمایشهایی که از نقطه نظر عملی قابل انجاماند، مقدور سازند.
مباحث مرتبط با عنوان