عملیاتهای چندگانه
به تركیب مقابل توجه كنید:
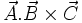
آیا باید اول ضرب داخلی را انجام داد یا خارجی را؟
اگر از چپ عمل كنیم با ضرب داخلی
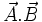
یك عدد میشود كه دیگر نمیتواند در
ضرب خارجی شود. پس در اصل مفهوم این عبارت همان
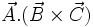
است. خُب بیایید ببینیم تعبیر هندسی این رابطه چیست.
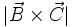
مساحت متوازیالاضلاع حاصل از
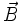
و
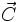
است. جهت

عمود بر صفحه
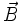
و
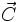
است. وقتی
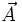
در آن ضرب داخلی میشود مقدار آن خواهد شد:
كه
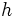
ارتفاع
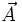
نسبت به صفحه
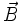
و
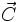
است و
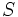
مساحت متوازیالاضلاع. پس مقدار
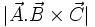
حجم متوازیالسطوح حاصل از
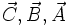
است. طبیعی است اگر این حجم را با جابجایی مكانهای
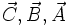
در
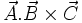
حساب كنیم تغییری نكند.
منتها حواسمان باید باشد كه ترتیب از جهت گردش (راستگردی یا چپگردی) ثابت بماند وگرنه مقدار كمیت منفی خواهد شد. برای این منظور كافی است صرفاً چرخشی انجام دهیم.
میتوان بفرم دیگری نیز این حاصلضرب سهگانه را نشان داد:
در این حالت هم میدانیم كه هر بار جابجایی سطرها، مقدار دترمینان را منفی میكند پس با دو بار جابجایی كه یك گردش خواهد شد علامت عوض نخواهد شد و اتحاد سابق مشاهده میشود. از جمله ضربهای سهگانه معروف
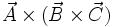
است كه محاسبه مستقیم آن چیزی نزدیك به فاجعه است. این مقدار بطور عجیبی در اتحاد «بك-كب» ساده میشود:
طبیعی است كه ابتدا ضربهای داخلی صورت میپذیرد و سپس عدد حاصل در بردار ضرب میشود چیزی شبیه این اتحاد را بعداً در آنالیز برداری خواهید دید.
مثال
نیروی مغناطیسی كه دو بار متحرك به اندازه
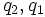
و بردارهای سرعت
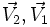
به هم وارد میكنند (برای سرعتهای خیلی كمتر از
) تقریباً از رابطه زیر تبعیت میكند:
كه
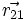
بردار مكان نسبی بار 2 به 1 است و
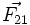
نیروی وارد بر 2 از بار 1 است. همچنین
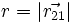
. نشان دهید كه
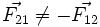
و قانون سوم نیوتن در این مورد برقرار نیست. (از مثالهای نقض مكانیك نیوتنی)
حل.
که طبق رابطه(بك-كب)است
چون
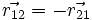
حال كه واضح است اگر
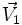
با
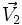
موازی نباشد قطعاً صفر نمیشود.
پیوند های خارجی
http://Olympiad.roshd.ir/physics/content/pdf/0030.pdf