|
این مطلب از بخش آموزش وبسایت المپیاد کامپیوتر رشد،انتخاب شده که با فرمت pdf نیز در وبسایت المپیاد رشدموجود میباشد. برای مشاهده این موضوعات در وبسایت المپیاد، به آدرس فهرست مطالب کامپیوتر مراجعه کنید. همچنین میتوانید با کلیک اینجا ، با ویژگیهای بخش آموزش این وبسایت آشنا شوید. |
اصل ناوردایی
در اینجا یکی از استراتژی های سطح بالا در حل مسایل را توضیح خواهیم داد. مسایل این قسمت در نگاه اول مشکل به نظر می رسند اما با حل چند مثال، روش کلی حل مسایل را به دست خواهیم آورد و خواهید دید که گاهی اوقات مسایلی که صورت آنها بسیار پیچیده است، چه باطن ساده ای دارند. در حقیقت روش حل مساله را تنها با حل مساله می توان آموخت. بنابراین توصیه می کنیم پس از مشاهده هر سوال ابتدا سعی کنید خودتان مسایل آن را حل کنید و سپس حل کتاب را مشاهده کنید.استراتژی اول حل مساله جستجوی قواعد ثابت است. در حل مساله های این فصل این قاعده را رعایت کنید:
اگر یک تکرار مشاهده کردید به دنبال یک قاعده ثابت بگردید.
در مسایل این فصل در هر مساله یک حالت اولیه (فضای ابتدایی) وجود دارد و عملی نیز تعریف شده که در هر گام انجام می شود و معمولاً یک حالت به عنوان هدف نهایی معرفی شده و سوال این است که: آیا می توان به این هدف نهایی رسید یا خیر؟ بنابراین مسایل این فصل 2 حالت دارند:1.مسایلی که رسیدن به حالت هدف آنها ممکن است: این دسته از مسایل (به نظر من) جالب تر هستند در این مسایل معمولاً به دنبال یک تابع اکیداً صعودی یا اکیداً نزولی برای هر گام می گردیم. پس از یافتن این تابع تقریباً 80% مساله حل شده است. پس از یافتن این تابع معمولاً مسایل به 2 روش حل می شوند.
الف.از آنجا که تابع یکنواست، در گام های مساله به حالت تکراری برنمی خوریم چون بایستی در این صورت رشد تابع در مواقعی به صورت عکس ادامه یافته باشد. اگر تعداد حالت های (فضای) مساله محدود باشد چون در هر گام به یک حالت جدید می رسیم پس این عمل نمی تواند بینهایت بار انجام شود و بالاخره این عمل متوقف می شود و معمولاً توقف عمل معادل حل مساله است.
ب.تابع یکنواست و قدر مطلق رشد آن از مقدار
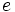 بیشتر است حالا اگر تابع مورد نظر از مقدار مشخصی بیشتر (یا کمتر) نشود در این صورت این عمل متوقف خواهد شد. در اینجا ذکر یک نکته لازم است. مقدار
بیشتر است حالا اگر تابع مورد نظر از مقدار مشخصی بیشتر (یا کمتر) نشود در این صورت این عمل متوقف خواهد شد. در اینجا ذکر یک نکته لازم است. مقدار 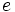 چرا لازم است: فرض کنید هدف ما عدد 2 است و حالت ابتدا عدد 1 است و در گام اول
چرا لازم است: فرض کنید هدف ما عدد 2 است و حالت ابتدا عدد 1 است و در گام اول  در گام دوم
در گام دوم 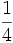 در گام سوم
در گام سوم  و ... به عدد 1 اضافه شود مشاهده می کنیم که همیشه می توان به عدد موجود عددی اضافه کرد و هیچ وقت هم این عدد به 2 نمی رسد. اینجا لزوم وجود
و ... به عدد 1 اضافه شود مشاهده می کنیم که همیشه می توان به عدد موجود عددی اضافه کرد و هیچ وقت هم این عدد به 2 نمی رسد. اینجا لزوم وجود 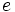 اثبات می شود.
اثبات می شود.
2.مسایلی که رسیدن به حالت هدف در آنها ممکن نیست: در این مسایل معمولاً رابطه ثابتی می یابیم که با هر عمل همچنان برقرار باقی می ماند اگر این رابطه برای حالت نهایی (حالت هدف) برقرار نباشد، چون تنها به حالت های ممکن است برسیم که این رابطه را ارضا می کنند، بنابراین به حالت نهایی نمی رسیم (به این روش استفاده از اصل هم خوانی هم می گویند).
مثال1
از نقطه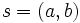 با فرض
با فرض 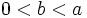 در صفحه شروع می کنیم و دنباله نقاط
در صفحه شروع می کنیم و دنباله نقاط 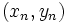 را بر طبق قانون زیر می سازیم:
را بر طبق قانون زیر می سازیم:
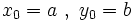
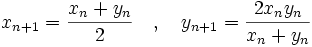
ثابت کنید با بزرگ شدن
 ،
، 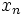 و
و  به سمت یک حد مشخص میل می کنند.
به سمت یک حد مشخص میل می کنند.
حل
در اینجا یافتن یک رابطه ثابت کار ساده ای است. از رابطه
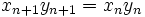 (که بسیار واضح است ) برای تمام مقادیر
(که بسیار واضح است ) برای تمام مقادیر  می توان نتیجه گرفت
می توان نتیجه گرفت 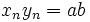 . در ابتدا داریم
. در ابتدا داریم 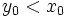 . این رابطه نیز به عنوان یک رابطه ثابت باقی می ماند. در حقیقت
. این رابطه نیز به عنوان یک رابطه ثابت باقی می ماند. در حقیقت  واسطه حسابی
واسطه حسابی  ،
، 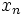 و
و  واسطه هندسی
واسطه هندسی  و
و 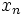 است: واسطه حسابی 2 عدد تنها وقتی با واسطه هندسی آنها مساوی است که 2 عدد با هم مساوی باشند و در غیر این صورت واسطه حسابی بزرگ تر است. چون
است: واسطه حسابی 2 عدد تنها وقتی با واسطه هندسی آنها مساوی است که 2 عدد با هم مساوی باشند و در غیر این صورت واسطه حسابی بزرگ تر است. چون 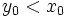 است، به ازای تمام مقادیر
است، به ازای تمام مقادیر  رابطه
رابطه 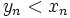 برقرار می ماند. پس برای تمام مقادیر
برقرار می ماند. پس برای تمام مقادیر  رابطه
رابطه
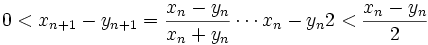
برقرار است. بنابراین
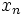 و
و  به ازای مقادیر بزرگ
به ازای مقادیر بزرگ  هر دو به سمت یک عدد که ما آن را
هر دو به سمت یک عدد که ما آن را 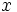 می نامیم میل می کنند.
می نامیم میل می کنند. 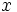 در رابطه
در رابطه  یا
یا  بایستی صدق کند.
بایستی صدق کند.
این مثالی از یافتن رابطه ثابت در مساله بود. توجه کنید که یافتن این روابط حل مساله نیست بلکه صرفاً ابزاری برای حل مساله است. اینکه چگونه از این روابط برای حل مساله استفاده نماییم نیز کاملاً ابتکاری است.
مثال2
فرض کنید یک عدد طبیعی فرد است. در ابتدا تمام اعداد
یک عدد طبیعی فرد است. در ابتدا تمام اعداد 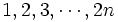 روی تخته سیاه نوشته شده اند. در هر مرحله 2 عدد دلخواه
روی تخته سیاه نوشته شده اند. در هر مرحله 2 عدد دلخواه 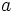 و
و 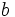 را از بین اعداد روی تخته سیاه پاک می کنیم و به جای آنها عدد
را از بین اعداد روی تخته سیاه پاک می کنیم و به جای آنها عدد  را می نویسیم. ثابت کنید عددی که در نهایت باقی خواهد ماند فرد است.
را می نویسیم. ثابت کنید عددی که در نهایت باقی خواهد ماند فرد است.
حل
فرض کنید
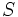 برابر مجموع اعدادی باشد که در هر مرحله روی تخته سیاه نوشته شده اند در ابتدا
برابر مجموع اعدادی باشد که در هر مرحله روی تخته سیاه نوشته شده اند در ابتدا  است که یک عدد فرد است. فرض کنید در یک مرحله 2 عدد
است که یک عدد فرد است. فرض کنید در یک مرحله 2 عدد 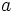 و
و 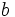 را انتخاب کنیم. بدون کاسته شدن از کلیت مساله می توانیم فرض کنیم
را انتخاب کنیم. بدون کاسته شدن از کلیت مساله می توانیم فرض کنیم 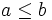 باشد در این صورت
باشد در این صورت 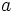 و
و 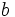 خط می خورند و به جای آنها
خط می خورند و به جای آنها 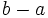 قرار می گیرد که درنتیجه مقدار
قرار می گیرد که درنتیجه مقدار 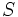 به اندازهُ
به اندازهُ  کاهش می یابد بنابراین زوج یا فرد بودن
کاهش می یابد بنابراین زوج یا فرد بودن 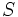 ثابت می ماند. در ابتدا
ثابت می ماند. در ابتدا 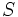 عددی فرد است بنابراین عددی که در نهایت باقی می ماند نیز فرد است.
عددی فرد است بنابراین عددی که در نهایت باقی می ماند نیز فرد است.
مثال 3
یک دایره را به 6 بخش تقسیم کرده ایم و در جهت خلاف حرکت عقربه های ساعت عددهای 0، 0، 0، 1، 0 و 1 در این بخش ها نوشته ایم. شما می توانید در هر مرحله به دو عدد که در 2 بخش مجاور قرار دارند یک واحد اضافه نمایید. آیا ممکن است به حالتی برسید که تمام اعداد نوشته شده با هم برابر باشند؟حل
برای حل مساله فرض می کنیم
 مجموع اعداد بخش های اول و سوم و پنجم و
مجموع اعداد بخش های اول و سوم و پنجم و  ، مجموع اعداد بخش های دوم و چهارم و ششم باشد روشن است که رابطه
، مجموع اعداد بخش های دوم و چهارم و ششم باشد روشن است که رابطه  همیشه برقرار است چون در هر گام به هر یک از
همیشه برقرار است چون در هر گام به هر یک از  و
و  یک واحد اضافه می شود. بنابراین امکان ندارد به حالتی برسیم که شش عدد با هم مساوی باشند چون در آن حالت
یک واحد اضافه می شود. بنابراین امکان ندارد به حالتی برسیم که شش عدد با هم مساوی باشند چون در آن حالت 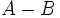 برابر 0 خواهد بود.
برابر 0 خواهد بود.

مثال 4
در یک پالمان هر نماینده حداکثر 3 مخالف دارد. ثابت کنید، این نمایندگان را می توان در 2 خانه قرار داد طوری که هر نماینده در خانهُ خود حداکثر 1 مخالف داشته باشد.حل
در ابتدا نمایندگان را به صورت دلخواه در 2 خانه قرار می دهیم. فرض کنید
 مجموع تعداد مخالفان افراد در خانه های خود باشد. فرض کنید
مجموع تعداد مخالفان افراد در خانه های خود باشد. فرض کنید  در خانه خود بیش از 1 مخالف داشته باشد بنابراین
در خانه خود بیش از 1 مخالف داشته باشد بنابراین  حداکثر یک مخالف در خانهُ دیگر دارد و می تواند به خانهُ دیگر برود. اگر خانهُ
حداکثر یک مخالف در خانهُ دیگر دارد و می تواند به خانهُ دیگر برود. اگر خانهُ  عوض شود مقدار
عوض شود مقدار  کم خواهد شد. (مقدار
کم خواهد شد. (مقدار  حداقل 2 واحد کمتر می شود) از آنجا که
حداقل 2 واحد کمتر می شود) از آنجا که  عددی طبیعی و محدود است این عمل نمی تواند همیشه ادامه یابد و بالاخره متوقف خواهد شد. یعنی بعد از چند مرحله مقدار
عددی طبیعی و محدود است این عمل نمی تواند همیشه ادامه یابد و بالاخره متوقف خواهد شد. یعنی بعد از چند مرحله مقدار  دیگر کاهش نمی یابد و درنتیجه در آنجا ما به نتیجه مطلوب رسیده ایم.
دیگر کاهش نمی یابد و درنتیجه در آنجا ما به نتیجه مطلوب رسیده ایم.
ملاحظه
در اینجا از یک ایدهُ جدید استفاده نمودیم. ما یک تابع اکیداً نزولی بافتیم که در هر مرحله مقدار آن کاهش می یابد و همیشه مقدار آن عددی صحیح و غیرمنفی است از آنجا که دنبالهُ نامتناهی اکیداً نزولی از اعداد صحیح و غیرمنفی وجود ندارد، این دنباله بایستی یک دنبالهُ متناهی باشد.
مثال 5
فرض کنید هر 4 عدد با هم مساوی نباشند از دنباله چهارتایی
با هم مساوی نباشند از دنباله چهارتایی 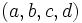 شروع می کنیم از این دنباله چهارتایی جدید
شروع می کنیم از این دنباله چهارتایی جدید  را می سازیم و همین عمل را با دنبالهُ جدید ادامه می دهیم. ثابت کنید کوچکترین عدد دنباله، می تواند از لحاظ قدرمطلق، به هر اندازه بزرگ شود.
را می سازیم و همین عمل را با دنبالهُ جدید ادامه می دهیم. ثابت کنید کوچکترین عدد دنباله، می تواند از لحاظ قدرمطلق، به هر اندازه بزرگ شود.
حل
فرض کنید به ازای هر
 ،
، 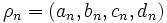 چهارتایی باشد که در مرحلهُ
چهارتایی باشد که در مرحلهُ  ام به آن رسیده ایم بنابراین برای
ام به آن رسیده ایم بنابراین برای 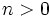 داریم:
داریم: 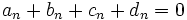 این یک رابطهُ ثابت است که شاید زیاد به ما کمک نکند ولی اگر ثابت کنیم دنبالهُ
این یک رابطهُ ثابت است که شاید زیاد به ما کمک نکند ولی اگر ثابت کنیم دنبالهُ  کران بالا ندارد در این صورت مسأله حل خواهد شد. می بینیم که رابطهُ زیر برقرار است.
کران بالا ندارد در این صورت مسأله حل خواهد شد. می بینیم که رابطهُ زیر برقرار است.
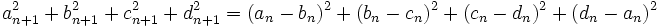
(1)
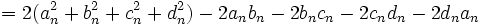
حالا از رابطهُ
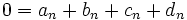 استفاده می کنیم:
استفاده می کنیم:
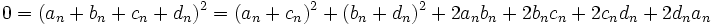
طرفین تساوی فوق و رابطهُ (1) را با هم جمع می کنیم تا رابطهُ زیر به دست آید:
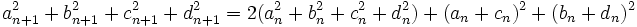
درنتیجه داریم:
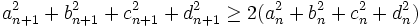
و درنتیجه به ازای هر
 داریم:
داریم:
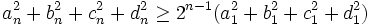
بنابراین مجموع توان دوم اعداد هر چهارتایی در هر مرحله در حال افزایش است و چون این مجموع همیشه عدد طبیعی است مقدار آن هر اندازه که بخواهیم بزرگ می شود. حالا نتیجه می گیریم بزرگترین عدد هر چهارتایی از لحاظ قدرمطلق، هر اندازه که بخواهیم می تواند زیاد شود. اما چون مجموع اعداد 4تایی ها بعد از مرحلهُ اول 0 است نتیجه می گیریم هم قدرمطلق کوچکترین عدد منفی و هم قدرمطلق بزرگترین عدد مثبت در حال افزایش است.
ملاحظه
اگر در این مسأله
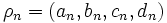 را نقطه ای در صفحهُ 4 بعدی فرض کنیم. متوجه می شویم که در هر مرحله، فاصلهُ نقطهُ جدید از مبدأ در حال افزایش است بنابراین فاصله از مبدأ تابع مهمی است که زمان هایی که با دنباله ای از نقاط سروکار داریم ممکن است مفید باشد.
را نقطه ای در صفحهُ 4 بعدی فرض کنیم. متوجه می شویم که در هر مرحله، فاصلهُ نقطهُ جدید از مبدأ در حال افزایش است بنابراین فاصله از مبدأ تابع مهمی است که زمان هایی که با دنباله ای از نقاط سروکار داریم ممکن است مفید باشد.
مثال 6
از نقطه با فرض
با فرض 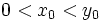 شروع می کنیم و در هر مرحله
شروع می کنیم و در هر مرحله  را به صورت زیر از
را به صورت زیر از 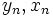 به دست می آوریم.
به دست می آوریم.
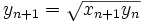

با استفاده از شکل 1 و نامساوی واسطه های حسابی و هندسی برای هر
 نشان دهید:
نشان دهید:



همچنین ثابت کنید
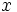 حد دنبالهُ
حد دنبالهُ 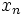 و
و  حد دنبالهُ
حد دنبالهُ  با هم مساوی اند.
با هم مساوی اند.
حل
در اینجا نیز اصل عدم تغییر به کمک ما می آید. به تغییرات
 و
و 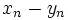 وقتی از مرحلهُ
وقتی از مرحلهُ  ام به مرحلهُ
ام به مرحلهُ 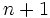 ام می رویم، توجه کنید:
ام می رویم، توجه کنید:
(1)
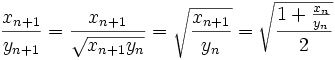
این رابطه ما را به یاد رابطهُ بین کسینوس نصف یک زاویه با کسینوس خود آن زاویه می اندازد:
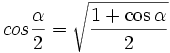
از آنجا که رابطهُ
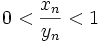 همیشه برقرار است می توانیم فرض کنیم
همیشه برقرار است می توانیم فرض کنیم  . بنابراین رابطهُ (1) به صورت زیر درمی آید:
. بنابراین رابطهُ (1) به صورت زیر درمی آید:
(2)
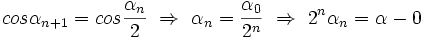
بنابراین می توان نتیجه گرفت:
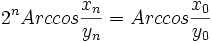
که همواره برای هر
 برقرار است.
برقرار است.
برای اینکه از ریشه دوم پرهیز کنیم به جای
 ،
،  را بررسی می کنیم.
را بررسی می کنیم.
داریم:

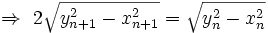
که با تکرار چند بارهُ آن به دست می آید:
(3)
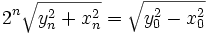
که این نیز رابطهُ مفید دیگری است.
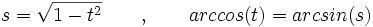
از شکل 2 و روابط (2) و (3) می توان نتیجه گرفت:

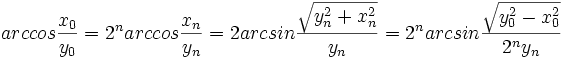
حد سمت راست وقتی
 به سمت بینهایت میل کند برابر
به سمت بینهایت میل کند برابر  است و درنتیجه رابطهُ زیر به دست می آید.
است و درنتیجه رابطهُ زیر به دست می آید.

ما این مسأله را به سختی می توانستیم بدون اصل عدم تغییر حل نماییم اسن مسأله یقیناً مسأله ای دشوار در برابر استاندارد رقابت های ریاضی می باشد.
مثال 7
هر یک از اعداد برابر 1 یا -1 هستند و داریم:
برابر 1 یا -1 هستند و داریم:
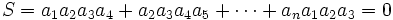
ثابت کنید
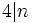 . .
. .
حل
این یک مسأله در نظریهُ اعداد است برای حل مسأله باز هم از اصل عدم همخوانی استفاده کنیم. یکی از
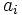 ها را به
ها را به 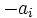 تغییر می دهیم و تغییرات
تغییر می دهیم و تغییرات 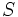 را بررسی می کنیم می بینیم که علامت 4 جملهُ متوالی که شامل
را بررسی می کنیم می بینیم که علامت 4 جملهُ متوالی که شامل 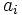 است تغییر خواهد کرد. اگر هر 4 جمله قبلاً هم علامت بودند،
است تغییر خواهد کرد. اگر هر 4 جمله قبلاً هم علامت بودند، 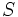 به اندازهُ
به اندازهُ  تغییر می کند اگر 2 تا مثبت و 2 تا منفی بودند،
تغییر می کند اگر 2 تا مثبت و 2 تا منفی بودند، 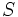 تغییری نمی کند و اگر 3 تا هم علامت بودند و یکی از علامت مخالف،
تغییری نمی کند و اگر 3 تا هم علامت بودند و یکی از علامت مخالف، 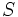 به اندازهُ
به اندازهُ 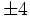 تغییر می کند. مشاهده می کنیم که باقیماندهُ
تغییر می کند. مشاهده می کنیم که باقیماندهُ 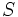 در تقسیم بر 4 نیز ثابت باقی می ماند. حالا تغییرات را طوری انجام می دهیم که تمام
در تقسیم بر 4 نیز ثابت باقی می ماند. حالا تغییرات را طوری انجام می دهیم که تمام 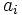 ها برابر 1 شود مشخص است که در این حالت
ها برابر 1 شود مشخص است که در این حالت 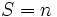 خواهد شد ولی باقیماندهُ آن به 4 تغییر نکرده است یعنی باقیماندهُ
خواهد شد ولی باقیماندهُ آن به 4 تغییر نکرده است یعنی باقیماندهُ  بر 4 برابر 0 است.
بر 4 برابر 0 است.
مثال 8
 سفیر به یک مهمانی دعوت شده اند که هر کدام حداکثر
سفیر به یک مهمانی دعوت شده اند که هر کدام حداکثر  دشمن در بین سفرای دیگر دارند. ثابت کنید این
دشمن در بین سفرای دیگر دارند. ثابت کنید این  سفیر را می توان دور یک میزگرد طوری نشاند که دو طرف هر سفیر، سفیرانی قرار گرفته باشند که با او دشمن نباشند.
سفیر را می توان دور یک میزگرد طوری نشاند که دو طرف هر سفیر، سفیرانی قرار گرفته باشند که با او دشمن نباشند.
حل
این مسأله دارای حلی با استفاده از نظریه گراف می باشد، اما اینجا ما سعی می کنیم با استفاده از پایان پذیری آن را حل کنیم: در ابتدا افراد را به صورت تصادفی دور میزگرد می نشانیم فرض کنید
 تعداد زوج های دشمن که کنار هم هستند، باشد. باید روشی ارائه دهیم که در هر مرحله باعث کاهش مقدار
تعداد زوج های دشمن که کنار هم هستند، باشد. باید روشی ارائه دهیم که در هر مرحله باعث کاهش مقدار  گردد. فرض کنید
گردد. فرض کنید  و
و  دو سفیر مجاور و دشمن باشند، به طوری که
دو سفیر مجاور و دشمن باشند، به طوری که  سمت راست
سمت راست  باشد (شکل 3) ثابت می کنیم افراد مجاور
باشد (شکل 3) ثابت می کنیم افراد مجاور 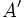 و
و 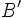 وجود دارد به طوری که
وجود دارد به طوری که 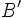 سمت راست
سمت راست 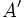 باشد و
باشد و  و
و  زوج های دوست باشند. می دانیم
زوج های دوست باشند. می دانیم  حداقل
حداقل  دوست در بین سفرای کشورها دارد. دور میزگرد
دوست در بین سفرای کشورها دارد. دور میزگرد  نفر نشسته اند که هر کدام دست راست یکی از این
نفر نشسته اند که هر کدام دست راست یکی از این  نفر قرار دارند. اگر همهُ این افراد با
نفر قرار دارند. اگر همهُ این افراد با  دشمن باشند
دشمن باشند  بیشتر از
بیشتر از  دشمن خواهد داشت بنابراین سفیر
دشمن خواهد داشت بنابراین سفیر 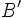 وجود دارد که سمت راست سفیر
وجود دارد که سمت راست سفیر 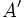 قرار گرفته باشد به طوری که
قرار گرفته باشد به طوری که و
و 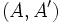 با هم دوست باشند.
با هم دوست باشند.
مطابق شکل 3 آرایش جدیدی از افراد با
 کمتر می توان ساخت. دقت کنید در شکل جدید، قرار گرفتن افراد بین
کمتر می توان ساخت. دقت کنید در شکل جدید، قرار گرفتن افراد بین  و
و 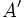 در جهت خلاف قرار گرفتن قبلی است.
در جهت خلاف قرار گرفتن قبلی است.

مسأله فوق یک مساألهُ نظریه گراف است و معادل این مسأله است که اگر در یک گراف ساده با
 رأس درجهُ هر رأس بزرگتر یا مساوی
رأس درجهُ هر رأس بزرگتر یا مساوی 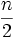 باشد آنگاه آن گراف دارای دور هامیلتونی است. روش حل دیگر این مسأله از طریق استقرا قهقرایی روی تعداد یال های گراف است. حالت پایهُ استقرا حالتی است که گراف ساده و کامل داریم.
باشد آنگاه آن گراف دارای دور هامیلتونی است. روش حل دیگر این مسأله از طریق استقرا قهقرایی روی تعداد یال های گراف است. حالت پایهُ استقرا حالتی است که گراف ساده و کامل داریم.
مثال 9
به هر رأس یک پنج ضلعی عدد صحیح را نسبت می دهیم به طوری که
را نسبت می دهیم به طوری که  در هر مرحله 3 عدد
در هر مرحله 3 عدد  که به ترتیب اعداد نسبت داده شده به 3 رأس متوالی پنج ضلعی هستند را انتخاب می کنیم به طوری که
که به ترتیب اعداد نسبت داده شده به 3 رأس متوالی پنج ضلعی هستند را انتخاب می کنیم به طوری که  باشد و سه تایی
باشد و سه تایی 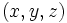 را تبدیل به سه تایی
را تبدیل به سه تایی 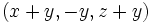 می کنیم و این کار را تا زمانی که عدد کوچکتر از صفری وجود داشته باشد ادامه می دهیم. آیا این عمل پایان می یابد یا خیر؟ (این مسأله مشکلترین مسألهُ المپیاد بین المللی ریاضی سال 1986 بود).
می کنیم و این کار را تا زمانی که عدد کوچکتر از صفری وجود داشته باشد ادامه می دهیم. آیا این عمل پایان می یابد یا خیر؟ (این مسأله مشکلترین مسألهُ المپیاد بین المللی ریاضی سال 1986 بود).
حل
این عمل همیشه پایان پذیر است. کلید اثبات (همانند مثال های 4 و 8) یافتن تابع صحیح
 است به طوری که مقدار
است به طوری که مقدار 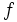 در هر مرحله که 3 عدد را عوض می کنیم کاهش یابد. از 11 دانش آموزی که این مسأله را حل کردند یکی تابعی مشابه تابع زیر معرفی کرد:
در هر مرحله که 3 عدد را عوض می کنیم کاهش یابد. از 11 دانش آموزی که این مسأله را حل کردند یکی تابعی مشابه تابع زیر معرفی کرد:
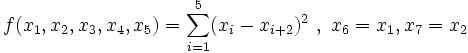
فرض کنید
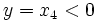 . در این صورت اگر
. در این صورت اگر 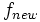 مقدار
مقدار 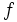 پس از انجام یک تغییر به مرکزیت
پس از انجام یک تغییر به مرکزیت 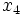 باشد و
باشد و 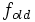 مقدار
مقدار 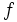 قبل از تغییر باشد داریم:
قبل از تغییر باشد داریم:

و از آنجا که
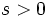 مقدار
مقدار  منفی است یعنی تابع
منفی است یعنی تابع 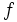 در هر مرحله در حال کاهش است. بنابراین اگر این عمل پایان ناپذیر باشد ما یک دنبالهُ نامتناهی اکیداً نزولی از اعداد صحیح و غیرمنفی یافته ایم که غیرممکن است.
در هر مرحله در حال کاهش است. بنابراین اگر این عمل پایان ناپذیر باشد ما یک دنبالهُ نامتناهی اکیداً نزولی از اعداد صحیح و غیرمنفی یافته ایم که غیرممکن است.
«برنالد چازل» از دانشگاه پرینستون این سوال را مطرح کرد: چند مرحله لازم است تا الگوریتم متوقف شود. او دنبالهُ نامتناهی
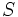 از مجموع هایی را در نظر گرفت که به صورت
از مجموع هایی را در نظر گرفت که به صورت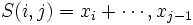 تعریف می شوند. (
تعریف می شوند. ( ) (
) ( ). وقتی به عنوان مثال
). وقتی به عنوان مثال 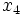 به
به  (همان گونه که در بالا مثال گفته شد) تبدیل می شود تنها جملهُ منفی که بین اعداد
(همان گونه که در بالا مثال گفته شد) تبدیل می شود تنها جملهُ منفی که بین اعداد 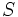 مثبت می شود
مثبت می شود 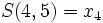 است که تغییر می کند و به
است که تغییر می کند و به  (همان گونه که در مثال بالا گفته شد) تبدیل می شود تنها جملهُ منفی که بین اعداد
(همان گونه که در مثال بالا گفته شد) تبدیل می شود تنها جملهُ منفی که بین اعداد 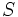 که منفی بود مثبت می شود. ار آنجا که
که منفی بود مثبت می شود. ار آنجا که  است،
است، 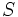 شامل تعداد متناهی عدد منفی می باشد بنابراین تعداد مراحل لازم برای توقف برابر تعداد اعداد منفی داخل
شامل تعداد متناهی عدد منفی می باشد بنابراین تعداد مراحل لازم برای توقف برابر تعداد اعداد منفی داخل 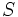 می باشد همچنین دیدیم که نیازی به صحیح بودن مقدار
می باشد همچنین دیدیم که نیازی به صحیح بودن مقدار 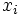 ها هم نیست.
ها هم نیست.
ملاحظه
جالب است که یک فرمول را با کامپیوتر بیابیم که این فرمول برای هر ورودی
 از اعداد تعداد مراحل لازم تا زمان توقف را بیابد. یافتن این فرمول برای حالت های که
از اعداد تعداد مراحل لازم تا زمان توقف را بیابد. یافتن این فرمول برای حالت های که 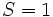 است چندان مشکل نیست برای مثال برای ورودی
است چندان مشکل نیست برای مثال برای ورودی 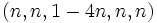 تعداد مراحل
تعداد مراحل 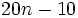 است.
است.
مثال 10 . کاهش مربع ها (یک تحقیق تجربی)
از چهارتایی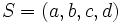 از اعداد صحیح و مثبت شروع می کنیم و چهارتایی جدید
از اعداد صحیح و مثبت شروع می کنیم و چهارتایی جدید 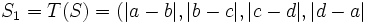 را از
را از 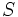 به دست می آوریم به همین ترتیب دنبالهُ نامتناهی
به دست می آوریم به همین ترتیب دنبالهُ نامتناهی  را می سازیم آیا همیشه در این دنباله ها به چهارتایی های
را می سازیم آیا همیشه در این دنباله ها به چهارتایی های 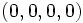 می رسیم.
می رسیم.
حل
برای اینکه جواب را حدس بزنیم چند مثال شروع می کنیم:



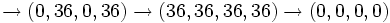
مشاهدات
(1)
اگر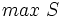 را بزرگترین عضو 4 تایی
را بزرگترین عضو 4 تایی 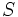 تعریف کنیم در این صورت:
تعریف کنیم در این صورت:
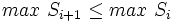
و همچنین تا زمانی که
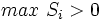 داریم:
داریم:
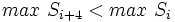
اگر این نامساوی ها اثبات شود، مسأله ثابت شده است.
(2)
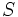 و
و  (4 تایی که از ضرب اعداد
(4 تایی که از ضرب اعداد 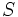 در عدد
در عدد 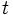 به دست می آید) دارای یک طول عمر می باشند.
به دست می آید) دارای یک طول عمر می باشند.
(3)
بعد از 4 مرحله هر 4 عدد به دست آمده حتماً زوج خواهند بود. برای اثبات این نکته می توانیم محاسبات را به پیمانهُ 2 انجام دهیم و تمام حالت ها را آزمایش کنیم به خاطر اینکه تغییر دوری جای 4 تایی ها تأثیری در استدلال ندارد تنها چند حالت ساده را لازم است آزمایش کنیم:
و
بقیه مشابه بالا 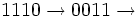
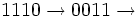
ملاحظه
در اثبات مشاهدهُ (3) از تقارن دوری استفاده کردیم ما همیشه بایستی بتوانیم در صورت امکان از این ایده استفاده کنیم. البته این بخش به این موضوع اختصاص ندارد.
مشاهدهُ (3) اثبات شد. پس حداکثر بعد از 4 مرحله ما با 4 عدد زوج سروکار داریم و حداکثر بعد از 8 مرحله هر جمله مضرب
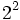 خواهد بود و ... و بعد از
خواهد بود و ... و بعد از 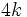 مرحله هر عدد دنباله مضرب
مرحله هر عدد دنباله مضرب  خواهد بود. اگر
خواهد بود. اگر  را طوری تعیین کنیم که
را طوری تعیین کنیم که 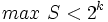 باشد در این صورت چون بیشترین عدد
باشد در این صورت چون بیشترین عدد 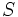 در چهار تایی های بعدی بزرگتر نمی شود بنابراین پس از
در چهار تایی های بعدی بزرگتر نمی شود بنابراین پس از 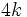 مرحله بایستی هر 4 عدد برابر 0 باشد (چون بعد از
مرحله بایستی هر 4 عدد برابر 0 باشد (چون بعد از 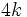 مرحله تمام اعداد مضرب
مرحله تمام اعداد مضرب  هستند ولی همگی از
هستند ولی همگی از  کوچکترند بنابراین باید 0 باشند.) . اگر مشاهدهُ اول هم اثبات شود می توان روش دیگری برای حل مسأله به دست آورد. برای اثبات مشاهدهُ اول می توان از اصل اکسترمال استفاده کرد انتخاب عنصر ماکزیمال! که در بخش 3 به آن می پردازیم.
کوچکترند بنابراین باید 0 باشند.) . اگر مشاهدهُ اول هم اثبات شود می توان روش دیگری برای حل مسأله به دست آورد. برای اثبات مشاهدهُ اول می توان از اصل اکسترمال استفاده کرد انتخاب عنصر ماکزیمال! که در بخش 3 به آن می پردازیم.
نتایج
الف
اگر از اعداد حقیقی شروع کنیم برای مثال:
می توان نتایج خاصی به دست آورد. که هنوز اثبات نشده است. آیا همیشه به
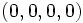 می رسیم؟ فرض کنید
می رسیم؟ فرض کنید  داریم:
داریم:

اگر
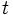 به گونه ای اختیار شود که
به گونه ای اختیار شود که  شود. این عمل هرگز پایان نمی یابد (برای مثال اگر
شود. این عمل هرگز پایان نمی یابد (برای مثال اگر 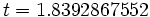 ) همچنین این مقدار
) همچنین این مقدار 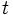 با صرف نظر از تغییراتی به صورت
با صرف نظر از تغییراتی به صورت 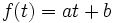 منحصر به فرد خواهد بود.
منحصر به فرد خواهد بود.
ب
از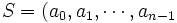 شروع می کنیم و فرض می کنیم
شروع می کنیم و فرض می کنیم 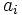 ها اعداد صحیح غیرمنفی
ها اعداد صحیح غیرمنفی
هستند. برای
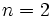 پس از 1 مرحله به
پس از 1 مرحله به  می رسیم. برای
می رسیم. برای 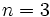 داریم:
داریم:
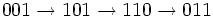
همچنین برای
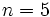 داریم:
داریم:


که یک حلقه به طول 15 می باشد.
مسئله
1.طول حلقه ها را برای (یا
(یا 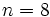 ) با دنبالهُ
) با دنبالهُ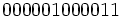 بیابید.
بیابید.
2.نشان دهید برای
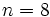 الگوریتم با ورودی
الگوریتم با ورودی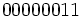 متوقف می شود.
متوقف می شود.
3.نشان دهید برای
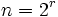 همیشه به دنبالهُ
همیشه به دنبالهُ  می رسیم و برای
می رسیم و برای 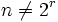 همیشه به دنباله ای از حلقه ها تکرار شونده می رسیم که شامل تنها 2 عدد می باشند که یکی 0 و دیگری غیرصفر است برای اثبات این قضیه می توان از اثبات مشاهدهُ 2 استفاده کرد.
همیشه به دنباله ای از حلقه ها تکرار شونده می رسیم که شامل تنها 2 عدد می باشند که یکی 0 و دیگری غیرصفر است برای اثبات این قضیه می توان از اثبات مشاهدهُ 2 استفاده کرد.
4.فرض کنیم
 حداکثر طول حلقهُ تکرار شونده برای
حداکثر طول حلقهُ تکرار شونده برای 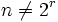 باشد ثابت کنید
باشد ثابت کنید  .
.
5.ثابت کنید که برای
 های فرد دنبالهُ
های فرد دنبالهُ 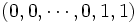 از همان ابتدا روی حلقهُ تکرار شونده است.
از همان ابتدا روی حلقهُ تکرار شونده است.
6.جبری کردن. به دنبالهُ
 چندجمله ای
چندجمله ای  را اختصاص می دهیم که در آن
را اختصاص می دهیم که در آن  (
(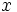 یکی از ریشه های
یکی از ریشه های  ام عدد 1 است در بحث اعداد مختلط ثابت می شود عدد 1،
ام عدد 1 است در بحث اعداد مختلط ثابت می شود عدد 1،  تا ریشهُ
تا ریشهُ  ام متمایز دارد) در این صورت چندجمله ای
ام متمایز دارد) در این صورت چندجمله ای  به دنبالهُ
به دنبالهُ 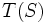 تعلق دارد. آیا می توانید از این جبری کردن استفاده نمایید.
تعلق دارد. آیا می توانید از این جبری کردن استفاده نمایید.
7.جدول زیر توسط کامپیوتر تولید شده است با استفاده از جدول زیر حدس هایی برای
 بزنید و آنها را اثبات کنید.
بزنید و آنها را اثبات کنید.
