|
این مطلب از بخش آموزش وب‌سایت المپیاد ریاضی رشد،انتخاب شده که با فرمت pdf نیز در وب‌سایت المپیاد رشدموجود می‌باشد. برای مشاهده این موضوعات در وب‌سایت المپیاد، به آدرس فهرست مطالب ریاضی مراجعه کنید. همچنین می‌توانید با کلیک اینجا ، با ویژگی‌های بخش آموزش این وب‌سایت آشنا شوید. |
قضایای متفرقه چندجمله‌ایها
در این فصل چند قضیه نسبتاً مهم که در فصول گذشته امکان آوردنشان نبود را بیان می‌کنیم. هر چند شاید برخی از این قضیه‌ها به مساله شباهت بیشتری داشته باشند، لکن به علت اهمیت آنها و ایده‌ای که در حل دارند بصورت قضیه بیان شده‌اند.قضیه1
فرض کنید
چند جمله‌ای درجه 
با ریشه‌های
(نه لزوماً متمایز) باشد، ثابت کنید بینو مشتق آن یعنی
، رابطه زیر برقرار است
اثبات.
بسادگی می‌توان نوشت
که
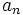ضریب بزرگترین توان
است. اکنون با توجه به فرمول محاسبه مشتق ضرب چندعبارت، می‌توان را بدین گونه بدست آورد:
-------- 
که همان صورت قضیه می‌باشد.
مثال1. (لهستان 1979)
فرض کنید چند جمله‌ای از درجه
است که ریشه حقیقی و متمایز
دارد. ثابت کنید:
اثبات.
با توجه به قضیه قبلی و محاسبه مقدار
می‌توان نوشت:
اگر قضیه درون‌یابی لاگرانژ را به خاطر آورید، متوجه شباهت بسیاری میان دستور درون‌یابی لاگرانژ و عبارت فوق که همان
می‌باشد، خواهید شد. اکنون فرض کنید چندجمله‌ای ثابت
را بخواهیم با فرمول درون‌یابی لاگرانژ بسط دهیم:
اگر در صورت قضیه قرار دهیم
می‌توان نوشت:
اکنون بوضوح ضریب جمله
در دو طرف برابر صفر خواهد بود، لذا در طرف چپ تساوی ضریب را بدینگونه محاسبه می‌کنیم:
که همان رابطه مورد نظر می‌باشد. پس اثبات مساله به پایان می‌رسد.
قضیه2
فرض کنیدچندجمله‌ای با ضرایب حقیقی باشد به نحویکه برای هر
، 
باشد. ثابت کنید دو چندجمله‌ای
با ضرایب حقیقی موجودند که برای آنها داشته باشیم:
اثبات.
ابتدا نشان می‌دهیم اگر
باشد، آنگاه باید ریشه‌های حقیقی، همگی دارای مرتبه تکرار زوج باشند. به عبارت دیگر امکان ندارد داشته باشیم
، زیرا در اینصورت با توجه به همواره مثبت بودن، برای 
داریم 
و برای
داریم، که نتیجه می‌دهد باید ریشه‌ای از
هم باشد، اما این نتیجه با فرض اینکه
مقدار تکرار ریشه 
است، تناقض دارد. لذا باید داشته باشیم
که
و
ها ریشه‌های حقیقی را شامل می‌شوند و
نیز تمام ریشه‌هایش مختلط است.
از طرفی بنابر قضیه3 مشاهده می‌شود که اگر
ریشه باشد، مزدوج آن یعنی 
نیز ریشه خواهد بود، لذا می‌توان را بصورت حاصلضرب چندجمله‌ایهای درجه دوم و با ضرایب صحیح تجزیه کرد که هر کدام بدین شکل‌اند:
اکنون با توجه به اتحاد لاگرانژ
می‌توان گفت که ضرب دو عبارت بصورت
یک عبارت به همان شکل است و چون ضرب یک دسته چندجمله‌ای بصورت
است، پس خود نیز بصورت جمع دو مجذور کامل قابل نوشتن می‌باشد، یعنی داریم
پس می توان
را اینگونه نوشت:
------- 
------- لذا اثبات قضیه کامل می‌شود.
قضیه3
نشان دهید اگر
ریشه‌ای با تکرر از چندجمله‌ایباشد، آنگاه ریشه‌ای با تکرار
از خواهد بود.
اثبات.
می‌توان نوشت
که داریم 
.
با محاسبه مشتق
از رابطه اخیر، خواهیم داشت:
و در ضمن داریم
. پس می‌توان نتیجه گرفت که ریشه‌ای با تکرر
از چندجمله‌ای می‌باشد.
در ادامه بحث لازم است بطور مختصر برخی از خواص چندجمله‌ایهای با ضرایب حقیقی را یادآوری کنیم:
خاصیت1
فرض کنید
، در اینصورت اگر زوج باشد، علامتبرای 
، موافق علامت
می‌باشد، و اگر فرد باشد و 
، باز هم علامتو موافق هم است، اما اگر
آنگاه علامت و متضاد هم خواهد بود. (این نکات براحتی با خواص ابتدایی حد و پیوستگی قابل اثبات می‌باشند.)
خاصیت2
هر چند جمله‌ای جزء توابع پیوسته است. لذا با توجه به قضیه مقدار میانی و خاصیت1، می‌توان نتیجه گرفت که اگر یک چندجمله‌ای ریشه حقیقی میانی و خاصیت 1، می‌توان نتیجه گرفت که اگر یک چندجمله‌ای ریشه حقیقی نداشته باشد، آنگاه درجه‌اش باید زوج باشد. زیرا برای چندجمله‌ایهای با درجه فرد مانند، مقادیر
دارای علامت مختلف هستند، لذا حتماً در بازه
یک ریشه خواهد داشت.
خاصیت3
از آنجا که تعداد ریشه‌های هر چند جمله‌ای محدود بوده و با درجه آن چندجمله‌ای برابر است، لذا نمودار تابع چندجمله‌ای بعد از بزرگترین ریشه حقیقی و یا قبل از کوچکترین ریشه حقیقی، محور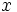
ها را قطع نمی‌کند. به عبارت دیگر در این نواحی، علامت چندجمله‌ای ثابت می‌ماند و با توجه به خاصیت 1 می‌توان در
علامت آنرا تشخیص داد. پس مقداری مانند
می‌توان به نحوی یافت که برای 
و
علامتثابت بماند.
خاصیت4
چون تابعی پیوسته و مشتق‌پذیر است و مشتق آن یعنی هم یک چند جمله‌ای است با درجه یکی کمتر از درجه، لذا اگر از خاصیت 3 در مورد استفاده کنیم بدست می‌آید که عددی مانند
وجود دارد که علامت برای و یا ، همواره مثبت و یا منفی می‌ماند. لذا می‌توان برای به این نتیجه رسید که در همان بازه و یا ،اکیداً صعودی و یا اکیداً نزولی خواهد بود.
قضیه4
اگر
و دو چندجمله‌ای باشند که معادله
، به ازای هیچ 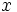، جواب نداشته باشد، انگاه یا همواره داریم
و یا
اثبات.
چندجمله‌ای
را تعریف می‌کنیم. با توجه به فرض قضیه، هیچ ریشه‌ای نخواهد داشت. لذا علامت یا همواره مثبت است و یا منفی، زیرا اگر در دو نقطه متمایز دارای علامتهای مختلف باشد، در بازه میان این دو نقطه حتماً در جایی صفر شده است. لذا اگر همواره
باشد داریم
، و اگر
باشد، خواهیم داشت
در ادامه چند قضیه مهم را بدون اثبات ذکر می‌کنیم. این قضیه‌ها در مورد توابع پیوسته هم برقرار می‌باشند، اما چون چندجمله‌ایها نیز توابعی پیوسته و مشتق‌پذیرند، می‌توان از آنها در این بخش نیز استفاده کرد.
قضیه5. (قضیه مقدار میانگین)
فرض کنید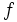
تابعی پیوسته و مشتق‌پذیر روی بازه
باشد. در اینصورت یک مقدار 
وجود دارد که برای آنها داشته باشیم:
توضیح. این قضیه بیان می‌کند که در یک نقطه
، شیب خط مماس بر تابع 
با شیب خط واصل میان نقاط 
و
برابر خواهد بود.
به عنوان حالت خاص مهمی از قضیه مقدار میانگین به قضیه زیر می‌رسیم:
قضیه6. (قضیه رول)
اگر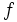روی بازه پیوسته و مشتق‌پذیر باشد و داشته باشیم 
، آنگاه عدد در بازه
موجود است به نحویکه:
به عنوان نتیجه ای از قضیه رول، می‌توان قضیه زیر را اثبات کرد.
قضیه7
اگرچندجمله‌ای باشد که دارای 
ریشه متمایز حقیقی
است. آنگاه نیز دارای
ریشه متمایز حقیقی خواهد بود و هر ریشه ، بین دو ریشه متوالی خواهد بود.
اثبات.
بوضوح داریم
، پس بنابر قضیه رول می‌توان گفت که در هر بازه
یک ریشه دارد و این همان چیزی است که درصدد اثبات آن بودیم.
دو قضیه زیر نیز در مورد رابطه بین ضرایب یک چندجمله‌ای و تعداد ریشه‌های مثبت و منفی ان چندجمله‌ای بیان شده‌اند.
قضیه8. (قاعده تعیین علامت دکارت)
فرض کنید
، اگر تعداد تغییر علامتها در دنباله
، تا باشد (ضرایب صفر را حذف می‌کنیم) آنگاهحداکثر ریشه مثبت دارد و در ضمن اختلاف تعداد ریشه‌های مثبت با ، عددی زوج خواهد بود.
نکته
توجه کنید که اگر ریشه‌ای مختلط باشد، منظور از مثبت بودن آن، مثبت بودن قسمت حقیقی ریشه می‌باشد.مثال2
فرض کنید
، آنگاه دنباله ضرایب غیرصفر عبارتند از
، چون در این دنباله تعداد تغییر علامت از مثبت به منفی و برعکس آن، تعداد 
است، لذا می‌توان نتیجه گرفت که تعداد ریشه‌های مثبت صفر، یک و یا دو تا است. اما چون اختلاف این تعداد با
، عددی زوج است، پس تعداد ریشه‌های مثبت تنها می‌تواند صفر و یا دو عدد باشد.
در قضیه8 ؛ ما تنها یک حد بالا برای تعداد ریشه‌های مثبت
ارائه دادیم. برای بدست آوردن تعداد دقیق ریشه‌های مثبت و منفی یک چندجمله‌ای، می‌توان قضیه بعدی را بکار بست. لکن مشاهده می‌شود، هزینه این محاسبه دقیق، زیادی محاسبات خواهد بود. ابتدا به تعریف زیر توجه کنید:
تعریف1. (جدول روت – هرویتز)
فرض کنید
برای این چند جمله‌ای، جدولی بفرم زیر تشکیل می‌دهیم:
در دو سطر اول جدول روت، ضرایب
بصورت یکی در میان نوشته شده‌اند. از سطر سوم به بعد، هر سطر از دو سطر بالایی خود بدین ترتیب بدست می‌آید، مثلاً برای سطح سوم داریم:
و برای سطح چهارم هم بصورت مشابه داریم:
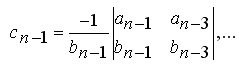
(دقت کنید علامت
نشانگر دترمینان می‌باشد.)
قضیه9. (معیار روت – هرویتز)
تعداد ریشه‌های مثبت چندجمله‌ای ، برابر با تعداد تغییر علامتهای اعداد واقع در ستون اول جدول روت – هرویتز متناظر با آن است. به عبارت دیگر تعداد تغییر علامتها در دنباله 
برابر تعداد ریشه‌های مثبتخواهد بود.
مثال3
همان چند جمله‌ای مثال قبل را در نظر بگیرید
، جدول روت هرویتز اینگونه تشکیل می‌شود:
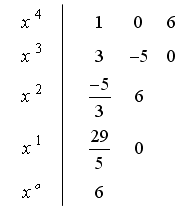
(دقت کنید که اگر عددی در هر مرحله در جدول وجود نداشت، مقدارش برابر صفر خواهد بود) اکنون با توجه به ستون اول جدول داریم
، که مشاهده می‌شود تعداد تغییر علامتها در آن برابر 2 می‌باشد. پس چندجمله‌ایدقیقاً دو ریشه مثبت دارد.
مثال4
چندجمله‌ای درجه سه
را در نظر بگیرید. می‌توان جدول روت را بدین شکل تشکیل داد:
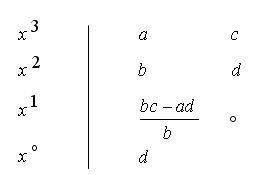
اگر فرض کنیم
است، آنگاه در صورتیکه
همگی مثبت باشند، چندجمله‌ای هیچ ریشه مثبتی نخواهد داشت.
نتیجه
چندجمله‌ای
، که در آن علامتهای 
مختلف است. حداقل یک ریشه مثبت دارد.
اکنون در پایان فصل چندمثال را بررسی می‌کنیم.
مثال5. (آمریکا 1983)
ثابت کنید به شرط
همه ریشه‌های معادله
نمی‌توانند حقیقی باشند.
اثبات.
اگر چندجمله‌ای
بخواهد 5 ریشه حقیقی داشته باشد، بنابر نتیجه قضیه رول که در قضیه7 بیان شد، باید مشتق آن یعنی دارای 4 ریشه حقیقی باشد و مشابهاً 
باید هر کدام بترتیب دارای 3 و 2 ریشه حقیقی باشند. با مقداری محاسبه می‌توان بدست آورد:
اگر دلتای این معادله درجه دوم را تشکیل دهیم، بدست می‌آید:
برای اینکه
ریشه‌های حقیقی داشته باشد، باید داشته باشیم
، که نتیجه می‌دهد 
، که بوضوح با فرض مساله تناقض دارد، لذا تمام ریشه‌های چندجمله‌ای نمی‌تواند حقیقی باشند.
مثال6. ( آلمان 1971)
فرض کنید چندجمله‌ایاز درجه و با ضرایب حقیقی، ریشه حقیقی نداشته باشد. ثابت کنید چندجمله‌ای
نیز برای هر عدد حقیقی
، ریشه حقیقی ندارد.
اثبات.
با گرفتن مشتق از طرفین رابطه داده شده، بدست می‌آوریم:
(توجه کنید درجه
برابر است و لذا داریم 
با مقایسه دو رابطه اخیر می‌توان بدست آورد
بدون کاسته شدن از کلیت مساله می‌توان فرض کرد ضریب
در، عددی مثبت باشد. لذا بنابر خاصیت‌هایی که در ابتدای همین فصل به آنها اشاره شد، چون ریشه حقیقی ندارد لذا همواره علامتی موافق علامت ضریب دارد، پس برای تمام
، مثبت خواهد بود و درجه آن زوج است. اکنون از برهان خلف استفاده می‌کنیم، فرض کنید دارای 
ریشه حقیقی
باشد. پس بنابر قضیه7 ، 
دارای
ریشه حقیقی مانند
است و داریم:
دو حالت برای
در نظر می‌گیریم:
حالت اول.
، در بزرگترین ریشه حقیقی یعنی
، مقدار را محاسبه می‌کنیم، داریم:
اما چون
برای مقادیر بزرگتر از
ریشه‌ای ندارد لذا همواره مثبت می‌ماند، به عبارت دیگر چون داریم 
، پس 
(زیرا درجه
فرد است)، که با توجه به مثبت بودن نتیجه می‌دهد: 
و این با نتیجه اولیه که برای تمام مثبت است، تناقض دارد.
حالت دوم.
، در کوچکترین ریشه حقیقییعنی 
، مقدار را محاسبه می‌کنیم:
باز هم چون درجه
عددی فرد است لذا علامت 
با علامت 
یکی است و لذا علامت منفی است که باز هم با فرض بدست می‌آید: 
، و این تناقض می‌باشد. لذا در نهایت فرض اولیه مبنی بر اینکه ریشه حقیقی دارد، اشتباه می‌باشد.